KOMBINATORIKA NA LAKŠI NAČIN – :)
Šta biste uradili sa novcem koji dobijete na loto premiji? Hmm, lepa tema za razmišljanje. Međutim, koje su šanse da dobijete premiju na lotou, odnosno, da od svih mogućih kombinacija izvuku baš vašu. Treba pogoditi jednu kombinaciju od … hmmm… mnogo J . Dakle, treba da izračunamo koliko ima svih mogućih loto kombinacija. E, tu na scenu stupa kombinatorika.
Kombinatorika u srednjoj školi može biti pravi bauk. Silne permitacije, kombinacije, varijacije i još ko zna šta. Baš kad pomislite da ste nešto razumeli dobijete zadatak koji nemate pojma kako da rešite. Kako najlakše razumeti elemente kombinatorike? Kako shvatiti kombinacije, permutacije i varijacije? I, na kraju, kako sve to primeniti u konkretnim zadacima?
Na sva ova pitanja pokušaću da odgovorim što jednostavnije i što razumljivije. Uvedimo najpre neke osnovne oznake i formule.
FAKTORIJEL
Faktorijel nekog prirodno broja je proizvod svih prirodnih brojeva koji su manji ili jednaki njemu. Faktorijel označavamo uzvičnikom (n!) i računamo ga na sledeći način:
Dakle, kada treba da izračunamo faktorijel neko broja samo pomnožimo sve prirodne brojeve od 1 do tog broja. To znači da je faktorijel broja 5 jednak
|
Zadatak 1: Koliko je 8! Rešenje: |
Primetimo da važi:
odnosno:
Ovo možemo i dalje da nastavimo:
To znači da je:
Radi lakšeg računanja uzima se da je 0!=1.
BINOMNI KOEFICIJENT
Još jedan važan pojam je binomni koeficijent. Naziv “binomni koeficijent” potiče iz formule za razvijanje pirodnog stepena binoma, ali to nama ovde ne treba pa nećemu gubiti vreme na to 😉 .
Binomni koeficijent označavamo (čita se n nad k) i računamo po formuli
Dakle, za računanje binomnog koeficijenta potrebna su nam dva prirodna broja.
|
Zadatak 2: Koliko je Rešenje: . |
Vratimo se sada na kombinatoriku. Kombinatorika nam računa na koliko načina možemo da izaberemo elemente nekog skupa. Dakle, imamo neki skup, iz njega izdvajamo podskupove i brojimo ih. Tri osnovna elementa kombinatorike su: permutacija, varijacija i kombinacija. Da bismo ih prepoznali potrebno je da odgovorimo na dva pitanja:
| Da li su izabrani svi elementi početnog skupa? Da li je poredak izabranih elemenata bitan? |
Kada odgovorimo na ova dva pitanja znaćemo da li je u pitanju permutacija, varijacija ili kombinacija. J
PERMUTACIJE
Zamislite da tri knjige treba da stavimo na policu. Na koliko načina možemo da ih poređamo?
Ako označimo knjige brojevima 1, 2 i 3 dobićemo šest mogućih rasporeda (1-2-3, 1-3-2, 2-1-3, 2-3-1, 3-1-2 i 3-2-1). Dakle, tri knjige možemo rasporediti na ukupno 6 načina. Ovo i nije bilo teško.
Međutim, stvar nam se znatno komplikuje ako imamo više knjiga, na primer 15. Posmatrajmo zato ovaj primer kao permutaciju. Naime, od 15 knjiga iz početnog skupa svih 15 moraju da budu postavljene na policu i bitan nam je njihov raspored na polici.
Odavde vidimo da će permutacija kao odgovor na gore spomenuta pitanja dati sledeće:
| Svi elementi početnog skupa JESU izabrani. Poredak izabranih elemenata JESTE bitan. |
Dakle, ako u zadatku na oba pitanja dobijemo potvrdan odgovor, u pitanju su permutacije.
Permutacije mogu da budu bez ponavljanja i sa ponavljanjem. Bez ponavljanja znači da su svi elementi u početnom skupu različiti (svih 15 knjiga koje treba da stavimo na polici su različite), dok permutacija sa ponavljanjem znači da neki elementi mogu da se javljaju više puta (na primer, u reči TATA slova T i A se javljaju po dva puta).
Broj permutacija od n elemenata bez ponavljanja (u oznaci P(n))računamo po formuli:
Pretpostavimo da da imamo 3 knjige među kojima su dve iste. Dve iste knjige možemo označiti brojem 1, a treću brojem 2. Sada ih na polici možemo rasporediti na samo 3 načina (1-1-2, 1-2-1 i 2-1-1). Dakle, dozvolimo li ponavljanje smanjiće nam se broj mogućih rasporeda.
Ako imamo n elemenata u početnom skupu u kome su m1, m2, m3,.. i mk brojevi istih elemenata elemenata, to jest koliko imamo istih elemenata koje vrste (pri čemu je m1+m2+m3+.. +mk=n), ukupan broj permutacija računamo prema formuli:
Dakle, ako imamo 15 knjiga na policu ih možemo rasporediti na
Kad vidim ovako veliki broj, moram da priznam da mi je drago da nisam morao da pišem sve moguće kombinacije. J
| Zadatak 3: Na koliko se načina 3 ista udžbenika matematike, 2 iste zbirke iz matematike i 1 radna sveska mogu poređati na polici.Rešenje: Odgovorimo najpre na dva važna pitanja. Vidimo da sve knjige idu na policu pa svi elementi početnog skupa jesu izabrani. Osim toga, poredak knjiga na polici jeste važan, pa zaključujemo da se radi o permutacijama.Takođe vidimo da se neke knjige ponavljaju pa su u pitanju permutacije sa ponavljanjem.Od ukupno knjiga imamo 3 ista udžbenika pa se prva knjiga ponavlja 3 puta, odnosno m1=3, dve iste zbirke te je m2=2 i samo jedna radna sveska pa je m3=1. Prema formuli za računanje broja permutacija sa ponavljanjem imamo: |
VARIJACIJE
Pretpostavimo sada da u jednom odeljenju od 25 učenika treba da izaberemo predsednika, sekretara i blagajnika. Dakle, od 25 učenika treba da odaberemo 3 i pritom je važno ko je predsednik, ko sekretar a ko blagajnik u odeljenju. Na koliko načina možemo napraviti ovaj izbor.
Ovde su u pitanju varijacije. Od 25 učenika u odeljenju mi biramo samo 3, pa nisu svi učenici izabrani. Takođe, važno je koga ćemo izabrati za predsednika, koga za sekretara a koga za blagajnike, obnosno, bitan je poredak našeg izbora. Odavde zaključujemo da će na dva važna pitanja varijacije dati sledeće odgovore:
|
Varijacije takođe mogu da budu sa i bez ponavljanja. Ako od n početnih elemenata biramo njih k, dobijamo varijacije od n elemenata k-te klase njihov broj označavamo kao ako su varijacije bez ponavljanja, i
ako su u pitanju varijacije sa ponavljanjem. Da ne dođe do zabune, u nekim udžbenicima se koriste i oznake
i
.
Broj varijacija k-te klase od n elemenata bez ponavljanja računamo po formuli:
U slučaju varijacija sa ponavljanjem imamo formulu:
U našem primeru pretpostavimo da isti učenik ne može da dobije dve funkcije (niko ne može da bude, na primer, i predsednik i blagajnik). Dakle, od 25 učenika biramo 3 bez ponavljanja učenika. To su varijacije od 25 elemenata treće klase bez ponavljanja pa imamo da je i
:
Zadatak 4: Koliko se trocifrenih brojeva može napisati pomoću cifara 1, 2, 3, 4, 5 i 6 ako se cifre
Rešenje: a) Dakle, od ponuđenih 6 cifara mi pravimo trocifrene brojeve (odnosno biramo po tri cifre) pri čemu se cifre ne ponavljaju. Dakle, sve cifre NISU izabrane i poredak izabranih JESTE bitan pa su u pitanju varijacije bez ponavljanja treće klase od 6 elemenata, odnosno odnosno, ukupno 120 brojeva. b) Ovde imamo isti slučaj ali ifre smeju da se ponavljaju pa je broj mogućih varijacija veći: |
KOMBINACIJE
Pretpostavimo sada da o jednom odeljenju od 25 učenika treba odabrati dva predstavnika za Učenički parlament. U ovom slučaju opet ne mogu svi učenici da budu izabrani (jer od njih 25 biramo samo 2), ali poredak nije bitan (jer oba člana parlamenta imaju jednake funkcije). Dakle, kombinacija nam na dva važna pitanja daje sledeće odgovore:
| NISU svi elementi početnog skupa izabrani. Poredak izabranih elemenata NIJE bitan. |
I kombinacije mogu biti sa ponavljanjem i bez ponavljanja. Kombinacije bez ponavljanja od n elemenata k-te klase obeležavamo sa i računamo po formuli:
Kombinacije sa ponavljanjem od n elemenata k-te klase (u oznaci) računamo formulom:
Dakle, u našem slučaju od 25 učenika biramo 2 pa su u pitanju kombinacije druge klase od 25 elemenata, a njih ima ukupno:
| Zadatak 5: Na koliko se načina iz špila od 32 karte mogu izvući 4 karte?
Rešenje: Od ukupno 32 karte mi biramo 4. Kako ne mogu biti izabrane sve karte i poredak nije bitan, zaključujemo da su u pitanju kombinacije od 32 elementa četvrte klase bez ponavljanja, pa je
|
ZAKLJUČCI
Sve gore navedeno možemo smestiti u jednu tabelu:
| Da li su izabrani svi elementi početnog skupa? |
Da li je bitan poredak među izabranim elementima? |
Formule za računanje |
|
| DA |
DA |
PERMUTACIJE |
Bez ponavljanja |
|
Sa ponavljanjem |
|||
| NE |
DA |
VARIJACIJE |
Bez ponavljanja |
|
Sa ponavljanjem |
|||
| NE |
NE |
KOMBINACIJE |
Bez ponavljanja |
|
Sa ponavljanjem |
Vratimo se sada na naš problem sa početka ovog teksta, dakle, koliko ima mogućih kombinacija u lotou. Podsetimo se da se u lotou od 39 brojeva bira 7 i nije važno kojim redom su brojevi izabrani. Posmatramo gornju tabelu i odgovaramo na pitanja: svi elementi NISU izabrani i poredak NIJE bitan. Dakle, zaključujemo da su u pitanju kombinacije. Osim toga, znamo da se brojevi ne vraćaju u bubanj pa se ne može desiti da se isti broj izvuče više puta, te su u pitanju kombinacije bez ponavljanja sedme klase o 39 elemenata. Dalje pratimo tablicu i nalazimo formulu po kojoj ćemo izračunati ukupan broj kombinacija:
U našem slučaju imamo:
Dakle, šanse da na lotou dobijemo premiju su 1 u 15380937, ili 1 u preko 15 miliona. Hmmm, može li kombinatorika i teorija verovatnoće bar malo da povećaju te šanse? 😉
Napomena: Ceo tekst možete preuzeti u pdf formatu ovde.
Svaka cast ze tekst… 🙂
Hvala. 🙂
Nadam se da će pomoći.
Nisu dobre formule za racunanje, proverio sam na matematiranju i u udzbeniku.
Hvala na primedbi, ali, molim Te, budi precizniji. Koje formule konkretno nisu dobre da ih odmah ispravim da ne bi unosile zabunu.
Provereno, sve formule rade i hvala mnogo, dosta mi je olakšao neke stavri sad pred prijemni ovaj tekst. 🙂
Nema na čemu. drago mi je da je tekst od koristi. Srećno. 😉
Svaka cast za tekst,ja nisam nista razumeo kad je nastavnica objasnjavala,a sutra imam kontrolni.Mislim da cu dobiti najmanje 4 😀
Hvala. Držim ti palčeve na kontrolnom sutra. 😉
ja nazalost jos uvek ne shvatam xD sta cu kad matematika nije moja stvar xD
tacnije,moj nastavnik je daao neki zadatak koji i posle ovoga ne znam da uradim…ako mozete da mi pomognete to bi bilo super.
Naravno 🙂 . Kako glasi zadatak?
Thx lik sve skuzio mjesec dana profa predaje ovo a ti mi pojasni sve u 5 minuta citanja ma ljubim te ;D
Hvala na podršci 🙂 . Drago mi je da ti je tekst pomogao.
Pozdrav
Pozdrav odlicno to radite stim sto smo mi to u skoli radili jos lakse Permutacije bez ponavljanja smo obelezavali kao n! varijacije naprimer 25 nad 3 samo 25x24x23 bez ovoga 25! kroz 22! i kombinacije takodje naprimer 39 7 kao 39×38…x32.. kroz 7! mislim da je tako lakse onako se izgubim u formulama 😀
U pravu si. Odlična ideja. Ubaciću oba načina računanja broja permutacija pa svako može da koristi formulu koja mu više odgovara.
Hvala i pozdrav. 🙂
hvalaa,sad cu procitati sve ovo i nauciti nadam se da cu dobro uraditi kontrolni 😀
Mnogo je dobro napisano i pomoglo mi je 100%!!!Ovde sam sve ukapirao za 10min a profesor predaje ovo 3-4 nedelje!!!HVALA!!!
Sada mogu da iskoristim ovo saznanje kako bih otkrio na koliko razlicitih nacina mogu da poginem na putu do skole 🙂
Otud tako mračne misli? Daj nešto vedrije. 😉
moze da se radi i bez formula,tako sam ja bar radila u skoli 😀
Da nije bilo ovog teksta ja bi pao kolokvij iz matematike. Bless your soul.
ma svaka cast, odavno nesto ovako sažeto a dooobro nisam procitala i napokon shvatila te permutacije, varijacije i kombinacije :)))))))))))))
Hvala najlepše. Drago mi je da je tekst pomogao.
Pozdrav.
Bojan
Sve pohvale za tekst, puno mi je pomogao.
Hvala najlepše. Drago mi je da je tekst od koristi.
Pozdrav.
Bojan
Hvala na ovom tekstu… Sve sam bolje shvatila…. Ali mi smo ucili da se permutacije ne mogu ponavljati… Kako se sad ovde mogu ponavljati?
Nema na čemu. Drago mi je da je tekst razumljiv.
Što se permutacija sa ponavljanjem tiče, one se javljaju kada se neki elementi u skupu koji permutujemo ponavljaju.
Na primer, koliko se trocifrenih brojeva može napisati od cifara 1, 1 i 2.
Ako koristimo formulu za permutacije bez ponavljanja dobićemo da je
P(3)=3!=3*2*1=6
Međutim, jedini trocifreni brojevi koji mogu da se napišu ciframa 1, 1 i 2 su 112, 121 i 211. Dakle, samo tri broja pa nam nešto nije u redu sa formulom. Problem je što nam je formula dva puta računala brojeve. Ako u broju 112 jedinice zamene mesta, opet se dobija broj 112. Formula za permutacije bez ponavljanja ne ume da “prepozna” ovakve situacije pa nam ne daje tačne rezultate.
Formula za permutacije sa ponavljanjem (cifra 1 se ponavlja 2 puta, a cifra 2 samo jednom) će nam dati:
P(3)=3!/(2!*1!)=6/2=3
Nadam se da je ovo pomoglo.
Pozdrav
Bojan
Svaka cast brate , mnogo lepo objasnjeno u kratkim crtama i najvaznije … ja nemam problema sa matematikom mada sad pomazem drugu da polozi pa sam ovo malo bio zaboravio , posle citanja ove prezentacije nije mi bio potreban nikakav udzbenik , stvarno svaka cast 🙂
Hvala najlepše. Drago mi je da je tekst pomogao.
Pozdrav.
Bojan
carski!!!
Hvala. 🙂
Pozdrav.
careeeeee, bas mi je ovo pomoglo, iako sam VI razred, koristi na tekmicenjima B)
Imam X elemenata (a, b, c..) od kojih svaki može da poprimi samo vrijednost 0 ili 1. Koliko je mogućnosti ako je X = 8, a koliko ako je X = 16. Koja je formula za računanje broja mogućnosti?
Hvala unaprijed na odgovoru.
Da budem plastičan… ako imam x broj različitih karata (niti jedna od njih nije ista), a svaka karta može da bude okrenuta licem ili naličjem (svaka od njih može da ima samo ove dvije vrijednosti – lice ili naličje), koliko je ukupno mogućnosti za X = 8 (karte označene sa: a, b, c, d, e, f, g, h), a koliko ukupno mogućnosti za X = 16 (tj. karte od a – s)?
Zahvaljujem još jednom.
Ili koliko se (x)cifrenih brojeva može napisati od cifara 1 i 2 za x = 16 i x = 32 i koja je formula?
Da li je odgovor 2 na x?
Tako je. Odgovor je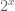 .
.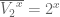 .
.
Naime, kako ne moraju svi elementi 1 i 2 da budu izabrani (jer možemo da izaberemo samo jedinice ili samo dvojke) i raspored elemenata jeste bitan, zaključujemo da su u pitanju varijacije x-te klase od 2 elementa, odnosno
Bravo Amire!
Inače, ovo je direktno povezano sa načinom na koji vaš računar pamti. Kako računar “zna” samo elemente 0 i 1 (dva elementa pa otud naziv binarni sistem) on može da upamti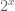 reči dužine x. 😉
reči dužine x. 😉
ja sam davno diplomirao matematiku i poneko mi dođe da mu pomognem.Do ovog momenta sam izbegavao kombinatoriku.. Hvala na divnom postu
Nema na čemu. Drago mi je da je tekst koristan.
Pozdrav.
eee, kad bi nama profesor zadao tako jednostavne zadatke 😦
I najsloženiji zadaci se razlažu na jednostavnije delove.
Ovaj tekst objašnjava kako rešiti te jednostavne delove.
Složeniji problemi se rešavaju u zavisnosti od situacije. 😉
Pozdrav
e brate hvala ti na ovom objasnjenju 🙂 samo reci hvale…ae sutra moram dobiti 5 iz amte na kontrolnom 😀
Hvala najlepše. Držim ti palčeve. 😉
Pozdrav.
Svaka cast na objasnjenju, izgubih vreme citajuci udzbenike a ovde sam shvatio za cas. Hvala!!!
Nema na čemu. 🙂
Hvala vama na komentarima.
Pozdrav
Bojan
Zdravo Bojane, Odlicno si ovo uradio, svaka cast.
Ovde sam stigao jer ocajnicki trazim resenje jednog zadatka. nadam se da mi mozes pomoci.
Dakle:
Na jedan teniski turnir se prijavilo 20 igraca. ako u prvom kolu svaki igrac dobije jdnog protivnika koliko mogucnosti imamo da odigramo to prvo kolo?
Unapred hvala sasa.
Hvala najlepše, Saša.
Tvoj zadatak me je jako zainteresovao (čak toliko da sam na nekoj svadbi pre par dana dobio ideju i krenuo da ga rešavam na salveti, pa dobio kritike od svoje lepše polovine 😀 ). Dobio sam neko rešenje, ali mi deluje previše komplikovano pa ću probati ovih dana da ga što pažljivije i pedantnije objasnim.
Hvala puno na zadatku i srdačan pozdrav.
Bojan
Veoma dobro napisano. Kratko. Jasno. I sve je obuhvaceno. Svaka cast.
Hvala najlepše. 🙂
Super objašnjeno… Svaka čast i hvala 🙂
Nema na čemu. Drago mi je da je tekst razumljiv.
Hvala na komentarima. 🙂
svaka ti cast care 🙂 sve je lepo objasnjeno 🙂
Hvala. 🙂
Fantasticno.Zivim u spaniji i ne razumem jos spanski ali idem u skolu 🙂 Ovo mi je resilo problem iz takozvane “Combinatorie” (na spanskom) .Sve je uredu sa formulama a tekst je prejednostavan. Svaka cast!
Hvala najlepše. Drago mi je da je tekst pomogao.
Potrudiću se da i nadalje tekstovi budu što jednostavnije napisani.
I ja nisam uspeo da nađem grešku u formulama, a kolega koji ih je prijavio se ne javlja.
Ako ih neko nađe, molim vas da mi ih prijavi. Hvala. 🙂
Pozdrav
svaka čast kralju, jako dobre temelje sa učenjem za faks sam postavio baš na ovome člaknu! pozdrav iz BiH
Hvala najlepše. Drago mi je da je tako.
Pozdrav za sve u BiH
Bojan
jos jednom super tekst, ali imam pitanje: na koliko nacina se cifre broja 123456 mogu presloziti da barem jedna cifra ostane na svome mjestu? pozdrav!
Hvala na ovom sajtu. Spasili ste me,dan pred test,nista nisam kapirala,sada je bolje. 🙂
Javicu kako je proslo na testu,ali hvala u svakom slucaju. 😀 ^^
Drago mi je da je tekst pomogao. Držimo ti palčeve na testu sutra. 😉
sutra imam test iz ovoga,nisam imala pojma šta,kako-sad mi je sve jasno!Stvarno svaka čast,odlično objašnjeno,a opet jednostavno 😀
Hvala najlepše. Nadam se da je tekst pomogao. 😉
Vrlo razumljiv, postupan, odličan tekst u svakom smislu. Sve pohvale!
Hvala najlepše. Trudio sam se da tekst bude što jednostavniji i razumljiviji, a opet dovoljno koristan da pomogne. Drago mi je ako sam bar delimično uspeo u tome.
Svaka cast za tekst, veoma pomaze..:)
Hvala najlepše. 🙂
Odlično! Hoćeš li staviti ubrzo i vjerojatnost tako pojednostavljenu ? Hvala 😀
Hvala najlepše. Krenuo sam sa pisanjem upravo teksta o verovatnoći, ali su me omele obaveze. Tekst će uskoro biti gotov.
Hvala punoo 😀
Nema na čemu. 🙂
svaka cast, savrseno objasnjeno 🙂
Hvala najlepše. 🙂
Mozete mi samo pojasniti bilo koji primer iz KOMBINACIJA.Ne razumem zasto oduzimamo gornji od donjeg broja..
Može, naravno.
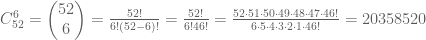
Najpre, izvinjavam se zbog kasnog odgovora, ali sam zbog prevelikog broja obaveza malo zapostavio ovaj blog.
Naime, kombinacije bez ponavljanja se računaju korišćenjem formule za binomni koeficijent koja je objašnjena u početnom delu teksta (odmah pole faktorijela). U samoj formuli se u imeniocu traži faktorijel razlike gornjeg i donjeg broja (odnosno http://upload.wikimedia.org/math/c/8/0/c80e0b1eec6d52e229fdafa91191f49d.png – slika je sa vikipedije).
Što se primera kombinacija tiče, zamislimo, na primer, da igramo tablić. Na koliko različitih načina možemo u prvom deljenju podeliti šest karata. dakle, od 52 karte u celom špilu biramo samo 6, pa nisu sve karte izabrane. Takođe, raspored kojim su podeljene je nebitan, što znači da su u pitanju kombinacije bez ponavljanja 6. klase od 52 elementa.
Može li ovo da pomogne?
Jasno..A jel se i kombinacije SA ponavljanjem racunaju preko iste formule za binomni koef.?
A sta se desava ako su svi elementi skupa izabrani, a poredak nije bitan? To jos jedan nacin kombinovanja ovih odgovora na pitanja..:D….dakle: JESU-JESTE, NISU-JESTE, NISU-NIJE i ovaj sto fali je JESU-NIJE…..
Sto je najgore, mislim da ovo kombinovanje JESTE-NIJE pripada bas toj neobjasnjenoj grupi….jer, svi elementi skupa {JESTE, NIJE} su izabrani, s tim sto njihov poredak nije vazan…a i da jeste vazan, bile bi to permutacije sa ponavljanjem, ciji bi rezultat dao 1/2….
Sta se ovde koji djavo desava? Molim za pomoc…
pozdrav!
Vaše pitanje je jako interesantno i hvala na njemu. To je, u stvari, najjednostavnija situacija. Naime, zamislite da od tri knjige treba da odaberete tri i nije bitno kojim redosledom. Pa to možete učiniti na samo jedan način. 🙂
A možemo tu situaciju da objasnimo i koristeći kombinacije. Naime, možete je posmatrati kao kombinacije n elemenata klase n. To nam, takođe, daje rezultat 1.
Takva situacija nije predviđena u tabeli jer bi tada za bilo koje n dobili rezultat 1, pa bi samo bespotrebno iskomplikovala tabelu. 😉
Nadam se da Vam je objašnjenje malo razjasnilo situaciju.
Pozdrav.
E ne znam jeli ti još aktivan blog, ali eto svejedno da probam 😀 imam jedan zadatak, “35 ljudi ulazi na stadion sa 40 ulaza, na koliko načina mogu ući pod uvjetom da svi uđu na različite ulaze?”, ja koliko sam skontao ne koriste se svi elementi, tj 35 ulaza od 40 se koristi, pošto svi ulazi moraju biti različiti, znači bez ponavljanja je, i redosljed nije bitan, znači trebale bi bt kombinacije bez ponavljanja, jeli to znači da je riješenje (40 nad 35) to ispadne 493 506, i hvala na jednostavnom objasnjenju kombinatorike
Tako je, Marko, s tim što treba biti oprezan da li je važan raspored osoba po ulazima, odnosno da li osoba A ulazi na ulaz 1, a osoba B na ulaz 2 ili obrnuto. U takvoj situaciji bi raspored ulaza bio bitan pa bi u pitanju bile varijacije.
Pozdrav i hvala na komentarima.
Pa to mi i je problem, ne znam da li je do mene ili do načina na koji profesor zadaje zadatke, evo imam ovaj “5 studenata sa pravnog fakulteta, 4 studenta sa računarastva i 3 sa pmf-a se natječu za ulazak na Senat sveučilišta. Na koliko je načina moguće napraviti izbor studentskih predstavnika ako njihov broj nije ograničen, uz uvjet da mora biti jednak broj sa prava i računarstva?” ovaj zadatak je bio na zadnjem ispitu, nisam siguran dali meni ovdje treba broj mogućnosti studenata koi će biti izabrani ili broj izbora koji su mogući. broj sstudenata sam računao preko kombinacija bez ponavljanja dobio sam 1125 mogućih, a broji mogućih izbora sam raspisao u biljeznicu i dobijem da je 19, tj 20-1 tj ona mogućnost kada niko nije izabran. Mislim da su mi oba rezultata tocna, u zavisnosti sta se trazi u zadatku. To me najvise zbunjuje, sta je pisac mislio reći 😛 Eto hvala još jednom, pozdrav.
Ne znam da li jos uvek posvecujete paznju ovom blogu,ali bolje da pokusam. Pre svega,odlicno ste sve to odradili,svaka cast.Ali,imam jedan mali problem,ne razumem kombinacije SA ponavljanjem,da li biste mogli da mi pojasnite?Unapred hvala! 🙂
Naravno 🙂 . Proučimo sledeći zadatak: koliko se različitih vrsta buketa od tri ruže može napraviti koristeći samo bele i crvene ruže?

Dakle, imamo dve vrste ruža (bele i crvene). Kako buket može da se napravi samo od ruža iste boje, možemo smatrati da nisu sve boje izabrane (ukoliko u buket stavimo samo crvene ruže, bele nisu izabrane). Sa druge strane, raspored ruža u buketu nije bitan. Ovo nas navodi na zaključak da su u pitanju kombinacije (NISU svi izabrani i poredak NIJE bitan). Osim toga, primetimo da slobodno možemo da izaberemo ruže iste boje, pa time boja može da se ponavlja. To znači da su u pitanju KOMBINACIJE SA PONAVLJANJEM. 🙂
Znači, imamo 2 elementa (dve boje) pa je n=2 i biramo 3 (tri ruže u buketu) pa je k=3. To nam daje rezultat:
Odavde dobijamo rezultat 4.
Ovaj rezultat možemo lako da proverimo. Naime, izlistajmo sve moguće kombinacije boja u buketu:
– 3 crvene ruže;
– 2 crvene i 1 bela ruža;
– 1 crvena i 2 bele ruže;
– 3 bele ruže.
Dakle, imamo četiri moguće kombinacije. 🙂
Nadam se da je odgovor pomogao.
Pozdrav.
Imam sutra pismeni profesor nam daje preteske zadatke. ..kao na primer : na zidu je okačeno deset slika koje se ne razlikuju. Na koliko načina možemo da skinemo 4 slike al da ne budu susedne? Možete li da mi postupno objasnite 🙂
Naravno. Pretpostavljam da sve četiri slike koje se skidaju ne smeju da budu susedne i da redosled skidanja slika nija bitan, s obzirom da su slike iste.

Izračunajmo najpre na koliko ukupno načina možemo skinuti slike (ne obazirući se da li su susedne).
Označimo slike na zidu, prema poziciji na kojoj se one nalaze, redom ciframa 0-1-2-3-…-9. Na koliko načina možemo da odaberemo 4 od datih 10 cifara, bez obzira na raspored.
Dakle, nisu sve slike skinute i redosled skidanja slika nije bitan pa zaključujemo da su u pitanju kombinacije 10 elemenata četvrte klase:
Oduzmimo sada sve situacije u kojima su slike koje se skidaju susedne, a to su sledeće situacije (koristimo prethodno definisane oznake slika):
0-1-2-3
1-2-3-4
2-3-4-5
3-4-5-6
4-5-6-7
5-6-7-8
6-7-8-9
Ima ih ukupno 7.
Dakle, od ukupno 210 kombinacija skidanja slika, 7 kombinacija nam ne odgovaraju jer su skinute susedne slike, pa nam ostaje 210-7=203 kombinacije.
Pozdrav.
Hvala puno 🙂 samo mi nije jasno kako ovako dobro znate matematiku ? 😀 i da, ovaj tekst mi je pomogao da kombinatoriku shvatim za 10 minuta iako sam u školi ovo radila pet časova i nista mi nije bilo jasno. … svaka čast i još jednom veliko hvala!!
Pozdrav, u slucaju da jos uvijek pratite pitanja, interesuje me sta je u situaciji kada su svi elementi pocetnog skupa izabrani, ali poredak nije bitan? Unaprijed hvala!
To je, u suštini, najjednostavniji slučaj. Naime, recimo da od tri čoveka treba odabrati tročlanu delegaciju, i da pritom raspored nije bitan. To možemo učiniti na samo jedan način (odabrati tri od tri 🙂 ).
Dakle, u tom slučaju, odgovor je uvek 1. 😉
Možda bi trebalo revidirati tekst i dodati i opis te mogućnosti? Šta mislite o tome?
Pozdrav.
Bojan
Hvala Vam puno. Prvi zadatak je od reci STATISTIK koliko moze da se sastavi reci sa istim slovima i istim brojem slova? ja sam faktorijel 9 podelila sa faktorijel 2*faktorijel3*faktorijel 2 i faktorijel1*faktorijel 1 i dobila 15 120. Drugi zadatak je: U studentskom domu ima 7 slobodnih soba. Na koliko nacina mogu 5 da studentkinja da ih podele I URADILA SAM TAKO STO SAM FAKTORIJEL 7 PODELILA SA (7-5)FAKTORIJEL I DOBILA 2520. Treci zadatak i poslednji je U tamnoj sobi u kutiji ima 4 crne, 6 sive i 2 braon carape. Ako izvucemo 2, koliko kombinacija istih boja ostaje? taj nisam umela da resim jer bih eventualno nala da iracunam koliko kombinacija postoji carapa koje moze da izvuce…Unapred, Hvala Vam puno
Svaka čast,može li broj tel da se čujemo vezano za ovaj predmet? Hvala
Hvala najlepše.
Ne zamerite mi, ali ne volim da ostavljam svoj broj telefona na netu (zbog mogućih zloupotreba; imao sam loša iskustva), ali mi se slobodno javite na mejl: boki_b77@yahoo.com.
Pozdrav
Bojan
Odlican tekst. Sve pohvale!
Prije ovoga teksta nisam mogao razlikovati permutacije,varijacije i kombinacije,ali sad mogu. 🙂
Hvala najlepše. 🙂
Raduje me kad vidim da je tekst pomogao nekome.
Bojan
Svaka cast. Mnogo sam muke imao sa ovim, nisam znao sta je sta. Sada je vec lakse, hvala puno.
Hvala :). Drago mi je da tekst pomaže.
Pozdrav
Svaka Vam cast za tekst! Sve pohvale!
Hvala najlepše. 🙂
Bojan
Potvrđujem da pomaže i na faksu 😀
Netko je spomenuo da formule nisu točne, ali provjerio sam i ne vidim greške.
Puno hvala na jasnim objašnjenjima!
Student iz Rijeke
Hvala najlepše na komentaru. Drago mi je da je tekst od koristi.
Srdačan pozdrav i mnogo sreće na studijama. 😉
Bojan
Hvala na tekstu. Citam komentare i ugledam ovaj zadatak za koji i dalje nisam nasao resenje. Pa ako ste Vi resili jel mozete sad odgovoriti? Zadatak glasi: Na jedan teniski turnir se prijavilo 20 igraca. ako u prvom kolu svaki igrac dobije jdnog protivnika koliko mogucnosti imamo da odigramo to prvo kolo?
Izvinjavam se zbog kašnjenja sa odgovorom.
Ovaj zadatak sam uspeo da rešim jako davno (a priča o njegovom rešavanju je anegdota za sebe; rešavao sam ga na nekoj svadbi na salveti 😀 – trenutak inspiracije je veoma nepredvidljiv) ali, na žalost, nisam sačuvao papire sa formulama tako da ću morati opet da se pozabavim ovim problemom prvom prilikom. Hvala najlepše što ste mi ukazali na to.
Pozdrav.
Bojan
Evo jedne varijante rešenja. Nisam stigao da proverim da li je tačno pa preporučujem da proverite rešenje. Rešenje je opšteg tipa i važi za paran broj takmičara. . Sada od preostalih
. Sada od preostalih 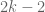 takmičara opet biramo 2, pa je broj mogućih kombinacija
takmičara opet biramo 2, pa je broj mogućih kombinacija  . Nastavimo li ovaj postupak preostaće nam na kraju samo 2 takmičara, odnosno
. Nastavimo li ovaj postupak preostaće nam na kraju samo 2 takmičara, odnosno  mogućih kombinacija.
mogućih kombinacija.


Pretpostavimo da na turniru učestvuje paran broj takmičara (2k) kako bi mogli da se podele na parove. Odaberimo najpre jedan par takmičara. Kako od 2k takmičara biramo samo 2 i redosled nije bitan, zaključujemo da su u pitanju kombinacije od 2k elementa klase 2, a njih ima
Zaključujemo da je ukupan broj parova jednak proizvodu broja ovih kombinacija, odnosno:
Skraćivanjem dobijamo:
Međutim, ovde moramo da budemo oprezni. Naime, neke kombinacije parova nam se ponavljaju. Na primer, posmatrajmo slučaj sa 4 takmičara: A, B, C i D. Ako najpre odaberemo par AB, dobićemo kombinaciju parova {AB, CD}. Međutim, ukoliko najpre odaberemo par CD, dobićemo kombinaciju parova {CD, AB}, što je, u stvari, ista kombinacija parova kao i prethodna. Dakle, moramo da izbacimo sve one kombinacije parova koje se ponavljaju.
Koliko ima takvih kombinacija parova?
Pretpostavimo da imamo 6 takmičara označenih sa A, B, C, D, E i F. Pretpostavimo da smo najpre odabrali par AB, zatim CD i na kraju EF. Ta kombinacija parova je ista kao i kombinacija u kojoj smo najpre odabrali par AB, zatim EF i tek na kraju CD. Na donjoj slici su prikazane svi mogući rasporedi izvučenih parova koji, u suštini, predstavljaju samo jednu kombinaciju parova:
U jednoj kombinaciji se, od ukupno 2k takmičara, može napraviti k parova takmičara. Svaka zamena mesta ovih parova predstavlja u stvari jednu permutaciju parova, a ovakvih permutacija ima k! (jer imamo ukupno k parova). .
.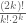 mogućih kombinacija parova.
mogućih kombinacija parova.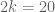 , odnosno
, odnosno 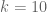 , pa ukupan broj mogućih kombinacija parova dobijamo primenom gornje formule:
, pa ukupan broj mogućih kombinacija parova dobijamo primenom gornje formule:
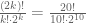
Zaključujemo da se u našoj formuli svaka kombinacija parova ponavlja k! puta, što znači da je dobijeni broj k! puta veći nego što treba da bude. To ispravljamo tako što ga podelimo sa k! i dobijamo:
Dakle, na turniru od ukupno 2k takmičara imamo
Kako je na našem turniru 20 takmičara, zaključujemo da je
Ovde se dobija jako veliki broj (654.729.079 ako ne grešim).
Molim vas da ovo rešenje uzmete sa rezervim o pokušate sami da proverite. Formula za male brojeve funkcioniše (2, 4, 6 i 8), ali ne mogu da stignem da je proverim za veće brojeve.
Ukoliko imate bilo kakvu primedbu na ovo rešenje ili nađete neko bolje rešenje, molim vas da nas obavestite. Sigurno će mnogo značiti onima koji rešavaju ovaj zadatak.
Hvala unapred. 🙂
Pozdrav.
Bojan
kako da izracunam -3 nad n? i a nad n?
Za negativne vrednosti koeficijenta k koristi se sledeća formula:

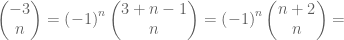
Odatle je:
hvala Vam najlepse 🙂
Nema na čemu. 🙂
Kako je sve jasno kad pravi “majstori” objašjjavaju. Obično profesori pišu knjige da dokažu nivo a ne da djacima bude jasno . Ja sam takodje profesor ali ekonomske grupe predmeta i slučajno mi je zatrebalo znanje iz kombinatorike, jasnije od ovog vašeg objašnjenja nisam našao na internetu, naročito što ste sve objasnili kroz primere. Hvala.
Hvala najlepše. Drago mi je da Vam je tekst pomogao.
Srdačan pozdrav.
Bojan
Pitanje:
Zadatak postavljen ovako:
1. A B
2. A B
3. A B
4. A B
5. A B
6. A B
7. A B
8. A B
9. A B
10 A B
Mora biti 10 u kombinaciji.
Koliko ima kombinacija?
Pozdrav i hvala unapred! 🙂
Ukoliko sam dobro razumeo, imamo 10 pozicija na kojima se može naći A ili B.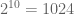 .
.
Dakle, na 10 pozicija biramo o jedan od 2 slova (A ili B).
U pitanju su varijacije sa ponavljanjem od 2 elementa klase 10, a njih je
Pozdrav 🙂
Hvala puno na rešenju 🙂
U kombinatorici sam uvek bila slaba.. Ni sad mi nije jasno zašto su ovo varijacije a ne kombinacije, jer poredak, mislim, nije bitan 😀
Svaka Vam cast!!!!
Hvala najlepše. 🙂
Možete li mi pomoći da rešim zadatak? On glasi: (x+2)!/ (x-1)! = 120. Pokušavala sam da ga rešim i nikako nisam uspela, u rešenjima piše da je rezultat 4. Hvala unapred 🙂
Možda ovo može da pomogne:
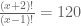
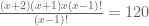


Skraćivanjem dobijamo:
Kako je:
Zaklučujemo da je x = 4
Pozdrav
Samo da Vas pitam kako da znam da li je poredak bitan..
Razmislite da li se, menjanjem poretka među izabranim elementima, menja i sam izbor.
Na primer, od cifara 1, 2, 3 i 4 pravimo dvocifrene brojeve. Dakle, od 4 cifre biramo dve. Redosled je, u ovom slučaju, bitan jer ako odaberemo prvo cifru 1, pa onda cifru 2, dobijamo broj 12. Ako odaberemo prvo cifru 2, pa onda 1, dobijamo broj 21. Kako su 12 i 21 dva različita broja, nije svejedno koja će cifra biti na prvom, a koja na drugom mestu.
Zamislimo sada drugačiji primer, da od 4 čoveka treba odabrati dvočlanu delegaciju. Opet, kao i u prethodnom slučaju, od 4 elementa biramo 2, ali sada redosled nije biten. Naime, da li ćemo prvo odabrati Peru pa Miku, ili prvo Miku, pa onda Peru, nama je svejedno. Bitno je da Pera i Mika čine dvočlanu delegaciju. 🙂
Koliko ima desetocifr br deljivih sa 4 a u cijim zapisima ne ucestv cifre 0 2 4 6..kako ovo da znam da li je perm komb ili varijac hvala unapred
Ovde najpre definišemo skup cifara koje smemo da koristimo. Kako ne smemo da koristimo cifre 0, 2, 4 i 6, ostaju nam 1, 3, 5, 7, 8 i 9. Od ovih 6 cifara ravimo desetocifrene brojeve.
1. Dakle, iz skupa od 6 elemenata biramo njih 10. Očigledno ćemo cifre morati da ponavljamo, što znači da ne moramo da odaberemo sve od ponuđenih 6 cifara (možemo da izaberemo, na primer, broj 1.111.111.111 u kojem, osim cifre 1, nijedna druga cifra nije odabrana). To znači da nisu sve cifre obavezno odabrane.
2. Kako pravimo desetocifrene brojeve, pozicija svake cifre u zapiso broja je važna (na primer, brojevi 123 i 321 sastoje se od istih cifara, ali nisu isti brojevi), zaključujemo da je redosled izabranih cifara bitan.
Kako nisu svi elementi izabrani, a redosled jeste bitan, zaključujemo da su u pitanju varijacije, i to sa ponavljanjem. 🙂
Ja bih organizovao loto po sistemu permutacije, izvlačio bi se 39 brojeva od 39, pa bi se svaki izvučeni broj vraćao u bubanj. Hvala vam za objasnjenje.
Svaka cast na ovako jednostavno objasnjenju. Mnogo mi je pomoglo ❤
Jako,jako dobro sazeto!Hvala,pomaze!